PGIアクセラレータによる姫野ベンチマークの最適化手順(その2)
 GPGPU、CUDA、姫野ベンチマーク、PGIアクセラレータ、Fermi 性能
GPGPU、CUDA、姫野ベンチマーク、PGIアクセラレータ、Fermi 性能
前回のPGIアクセラレータによる姫野ベンチマークの最適化手順(その1)の続編です。本稿では、PGIアクセラレータのディレクティブによる最適化の最終段階である Kernel ループスケジューリングの方法について説明します。また、一般的な CUDA Kernel 性能の最適化方法についても説明します。最終的な性能は、PGI 10.4 コンパイラを使用して、55 GFLOPS の性能を記録しました。同じ Nehalem (2.67GHz) のCPU上では、1コアで 4.1 GFLOPS ですので、13.5倍の加速性能を得ています。
2010年7月10日 Copyright © 株式会社ソフテック 加藤
姫野ベンチマーク・プログラムへの適用(Kernelループスケジューリング最適化)
前回は、単純に PGIアクセラレータの領域指定ディレクティブを使用して GPU CUDA並列コードの作成方法を説明しました。今回は、さらに ループスケジューリング最適化を詳細に説明し、その適用方法についても説明します。その結果、PGIコンパイラ・ディレクティブだけで、どの程度の性能を出すことができるかを知っていただきたいと思います。
PGIアクセラレータによる姫野ベンチマークの最適化手順 コラム(全2回)
- その 1 :単純に簡単なPGIアクセラレータ用ディレクティブだけを適用
- その 2 :PGIアクセラレータのループスケジューリングの最適化の適用(本稿)
Performance Summary
最初に、今回 PGIアクセラレータコンパイラを用いて得られた性能を示します。姫野ベンチマークの実行に使用した計算サイズは、M (256 x 128 x 128) です。
| 作業(最適化)ステップ | GTX 480 | GTX 285 | |
|---|---|---|---|
| STEP 1 | 反復ループの内側にアクセラレータ計算領域ディレクティブ | 1.29 GFLOPS | 1.27 GFLOPS |
| STEP 2 | 反復ループの外側にアクセラレータ計算領域ディレクティブ | 24.20 GFLOPS | 18.29 GFLOPS |
| STEP 3 | STEP 2+データ転送Clauseを追加指定 | 24.41 GFLOPS | 23.62 GFLOPS |
| STEP 4 | 反復ループの内側にアクセラレータ計算領域を置き、別途、データ領域ディレクティブ使用 | 24.33 GFLOPS | 23.54 GFLOPS |
| STEP 5 | STEP 3+データ領域ディレクティブを別途指定 | 24.40 GFLOPS | 23.62 GFLOPS |
| STEP 6 | Kernel のスケジューリング最適化 (GTX480と285では異なる方法でチューニング) | 46.17 GFLOPS | 23.63 GFLOPS |
| STEP 7 | STEP 6 + 配列データのアラインメント(整列)調整 | 47.12 GFLOPS | 24.60 GFLOPS |
PGI 10.4コンパイラを用いて得られた性能も以下に示します。このリビジョンでは、55.7 GFLOPS を記録しています。同じ Nehalem (2.67GHz) のCPU上では、1コアで 4.1 GFLOPS ですので、13.5倍の加速性能を得ています。
| 作業(最適化)ステップ | GTX 480 | GTX 285 | |
|---|---|---|---|
| STEP 6 | PGI 10.4 で実行 | 53.13 GFLOPS | 23.77 GFLOPS |
| STEP 7 | STEP 6 + 配列データのアラインメント(整列)調整 | 55.78 GFLOPS | 25.38 GFLOPS |
性能実測するシステム環境について
まず始めに、性能実測に使用する私のテストマシン環境について説明します。
| ホスト側プロセッサ | Intel(R) Core(TM) i7 CPU 920 @ 2.67GHz x 1 プロセッサ |
| ホスト側メモリ | PC3-10600(DDR3-1333)2GB x 2 枚 |
| ホスト側 OS | Cent OS 5.4、カーネル 2.6.18-164.el5 |
| PGI コンパイラ | PGI 10.6 (PGI 2010) |
| GPU ボード1 | NVIDIA Geforce GTX480(Fermi)、1401.0 MHz clock, 1535.7 MB memory |
| GPU ボード2 | NVIDIA Geforce GTX285、1476.0 MHz clock, 1023.3 MB memory |
| NVIDIA CUDA バージョン | CUDA 3.0ドライバと3.0 Toolkit |
使用する Fortran 90 姫野ベンチマークプログラムと本稿での適用ステップの説明
使用する姫野ベンチマークプログラムは、Fortran90構文で記述された himenoBMTxp.f90 をベースとして使用します。このコラムで使用した各最適化ステップ毎のソースファイルは、前回のコラムのページからダウンロードできます。ベンチマークの実行条件等も前のコラムを参照して下さい。
前回の「その1のコラム」で説明したPGIアクセラレータの適用ステップは次の通りです。
- STEP1:単純に 並列の対象ループ・ブロックを !$acc region /end region で囲む、悪い例
- STEP2:反復ループの外側を !$acc region /end region で囲む
- STEP3:STEP2に明示的にホストとGPU間のデータ転送を指定するクローズ(Clause)を使用する
- STEP4:STEP 3 と同等な形態であるが、反復ループの内側にアクセラレータ計算領域を置き、別途、データ領域ディレクティブ使用する例
- STEP5:STEP 3 と同等な形態であるが、データ領域ディレクティブで別途指定する例
本稿コラムで説明する最適化適用ステップは次の通りです。
CUDA Kernel 性能の最適化方法について
さて、PGIアクセラレータによる最後の最適化は、「アクセラレータ計算領域」内の kernel パフォーマンスの最適化作業となります。一般的な CUDA kernel 性能の最適化には以下の 表-2 のような方法があります。実際の GPU のハードウェア構造のどの部分を最適化するかと言うことを表すために、最適化が反映される場所を 図-1 にも示しました。表-2 では、この最適化手法にユーザが関与できるかどうかと言う観点で、PGI Accelerator と PGI CUDA Fortran のプログラミングモデルを比較しています。PGI Accelerator はコード最適化の主導がコンパイラであるため、ディレクティブが用意された機能でしか、ユーザは最適化方法に関与できません。以下の中で、PGI accelerator の欄の「間接的に可能」というのは、プログラム上の配列のサイズの変更、次元の変更等を施すことで、間接的にコンパイラによって、GPU 上のデバイスメモリのアクセスの最適化がなし得ると言った状況を言っています。これは、実際のところはコンパイラがメモリ最適化を行うため、ユーザ自身がデバイスメモリ内の配列の構成や配置を直接制御できないと言うニュアンスです。PGI CUDA Fortran は CUDA ネイティブな言語となりますので、以下の最適化は自身でプログラムすることで可能となります。
| Kernel 性能 最適化の手法 | PGI Accelerator (Directive) | PGI CUDA Fortran | |
|---|---|---|---|
| ① | 配列データのアラインメント(配列の leading 次元を 16/32 wordの倍数にする) | 間接的に可能 | 直接可能 |
| ② | デバイスメモリのアクセスの最適化(コアレッシング) | 間接的に可能 | 直接可能 |
| ③ | Shared Memory を利用した明示的なキャッシュの利用 | コンパイラ検出 | 直接可能 |
| ④ | Kernel のスケジューリング最適化(ブロック、グリッド構成の変更) | 直接可能 | 直接可能 |
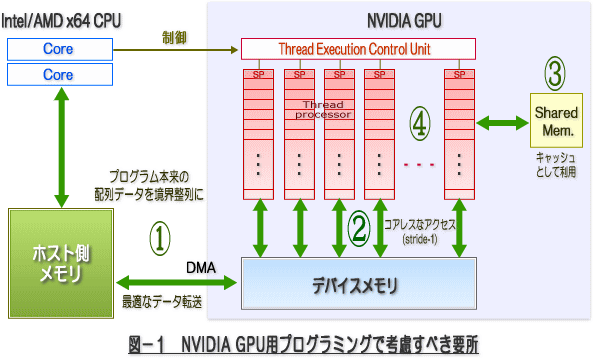
PGIアクセラレータ・プログラミングモデルを使用してユーザが明示的に最適化できる手法は、4番の「kernelスケジューリングの最適化」が主なものとなります。本稿では、この「kernelスケジューリングの最適化」について説明するのですが、その前に、他の最適化手法が、この姫野ベンチマークで具体的にどのように適用されたかを説明しましょう。
① 配列データのアラインメント
配列のサイズを変えると言う方法は、ユーザがメモリアクセスの最適化に関与できる一つの方法ですが、次元数の多い配列のメモリアクセスを有するプログラムでは、こうすれば性能が必ず良くなると言うことは断言できません。この姫野ベンチマークも3次元配列の隣接要素をアクセスする形ですので、メモリのアクセス性能を左右する複雑なアクセスパターンとなっています。これをいちいち分析して最適な配列構成を作ると言っても、これもかなり難解で、一般ユーザにとっては言ってみれば無駄な作業と言えます。一般には、いくつか配列の leading dimension のサイズを変えてみて、試行錯誤で性能を測定してみると言う方法が、GPU並列の場合は一番簡単な方法と言えましょう。配列の leading dimension とは、Fortran の場合は、A(i,j,k) と言う配列の場合は、列オーダーのため i 添字の次元を言います。C 言語の場合は、行オーダーのため k 添字となります。
NVIDIAの GPU の場合、デバイスメモリのアクセスでは、1回の命令で 16 words(これを "Superwords" と言う)をフェッチできるような機能を有しています。もし、この 16 words が同時に実行される 16 個のスレッドの各々で使用する形態をとる場合、これを「コアレッシングなアクセス」と言います。(Fermi すなわち Compute Capability 2.0 [CC 2.0] 以降は、32 words 単位のアクセスとなります。)但し、このようなアクセスを行うための必要条件が複数あります。これを「コアレッシング・アクセスのための条件」とも称しますが、例えば、一つのブロック内の先頭スレッドのアクセスするアドレスが、デバイスメモリ上で「64バイト」あるいは「128バイト」境界に整列(アラインメント)されていなければならないと言う条件があります。こうしたアラインメントがされていない場合、GPU ハードウェアの世代によってはアクセス性能が極端に下がる状況があります。昔のG8X・G9X系の Compute Capability 1.2 以前の GPU は、性能が 1/10 位に下がりました。GT200系 [CC1.3] の場合は、大分軽減されましたが、それでも 1/2 程度低下すると言われています。Fermi では、もう少し性能低下の加減が低下しているものと思います。ここで、言いたいことは、メモリ上の配列データの先頭アドレスは、できるだけ 16 or 32 words(CC 1.3 以前で64バイト、Fermiで128バイト)の境界にアライメントされていることが望ましいと言うことです。もし、この条件が満たされないと古い GPU では、性能が極端に低下します。
姫野ベンチマークではどうでしょう?具体的に配列の先頭アドレスのアライメントは、以下の箱枠内のように調整します。結論から言えば、姫野ベンチマークの場合は、こうした調整によって多少の効果は見えます(後述のステップ 7 の最適化)。実はこれには複雑な理由があり、簡単に表面的な配列の構造だけを見ただけでは判断できないと言うことです。従ってこうした場合は、サイズを変えて試行錯誤した方がベストフィットを見つけることができます。姫野ベンチの場合は、三次元のポイント・ヤコビの差分式となりますので、配列データのアクセス要素が非常に多くなります。その中にストライドを有したアクセスも当然含まれ、複雑なメモリアクセス特性を有するものとなります。最終的に性能を支配するのは、デバイスメモリ上のメモリアクセスの性能と言うことになりますが、メモリ内の個々の配列のネイティブなレイアウトに対するコアレッシング・アクセスの様態によって性能ががらりと変わります。これを、PGIアクセラレータ機能による高級言語上で、複雑な性能変化を予測しながら細かく制御することは不可能です。従って、配列の構造が簡単なプログラムであれば、こうした概念は性能最適化の一つの有効な方法ですが、3次元配列を使用する複雑な演算の場合は、何よりも以下にしめすような Padding 量を変化させてみて性能を観察する方法が一番実際的です。ただ、以前の GPU 程に、Fermi は大きく性能を低下させることはありません。
本稿の一番最後の最適化ステップ 7 で、Fermi対応のデータ境界のアラインメントの最適化を行った性能をお見せします。これが最終的に最も良い性能となりました。ソースの変更は、step6.F90 のソースに以下に示す実装を行いました。こうした Padding を行うべき配列添字は、基本的に SIMD(ベクトル)モードで実行する「スレッド・ブロック」で使用される threadidx インデックスに相当するものになります。(一般に、配列の leading dimension と言われている添字の調整を行います)
● 32ワード(128byte 境界)の倍数にするための配列 Padding 処理の例 subroutine readparam (略) call grid_set(size) (略) #ifdef PADDING halfwarpsize=32 ! Fermi の場合は 32 が良い。 CC 1.3の場合は 16でも良い。 imax=mimax-halfwarpsize #else imax=mimax-1 #endif jmax=mjmax-1 kmax=mkmax-1 (略) subroutine grid_set(size) (略) #ifdef PADDING halfwarpsize=32 #endif select case(size) (略) case("M") mimax=257 ! leading dimension のサイズを 32 の倍数へ mjmax=129 mkmax=129 (略) end select #ifdef PADDING ! 32 の倍数であり、かつ一番近い数字 mimax = (mimax + halfwarpsize) - mod(mimax,halfwarpsize) #endif
② デバイス・メモリのアクセスの最適化(コアレッシング)
デバイス・メモリ上のアクセスの最適化は、上記の配列データのアライメントの項で説明した「コアレッシング・アクセス」が可能となるように、デバイス・メモリ上で最適化することを言います。PGIアクセラレータでは、デバイス・メモリ上の配列は、ホスト側から転送された「配列形状」で割付られます。ホスト側から部分配列の転送を行った場合は、その部分配列の形状で配列のレイアウトがなされます。これで困ることは、ホスト上のプログラムで考えた配列要素のデータレイアウトとGPU上のレイアウトが異なることです。これは、すなわち「64バイト」あるいは「128バイト」境界と言った整列(アラインメント)の規則性が大きく異なってくると言うことです。この現象で、GT200シリーズ以前の GPU では、メモリアクセス性能が低下することが往々にしてあります。いわゆるコアレッシング・アクセスを阻害する状況が生まれる可能性があります(ただし、逆に、たまたま偶然に速くなると言うこともあるでしょう)。今回、この性能低下現象を見ることができます。上記の表-1 の GTX 285 の場合の STEP 2 の性能と STEP 3 の性能がそれです。STEP 2 はコンパイラデフォルトの配列データの部分転送のみを行った性能です。一方、STEP 3 は、ホスト側の配列の割付と同じ形状で全てのデータを明示的にGPUへ転送したときの性能です。明らかに大きな性能差があります。Fermiである GTX 480 は、こうした現象が生じていません。Fermi以降では、L2/L1キャッシュの利用もあり、データ・アラインメントによる性能低下傾向は緩和されているようです。
GTX 285 (CC 1.3) におけるメモリアクセスに関係する性能変化
最適化 STEP 2 18.29 GFLOPS (ホスト側から部分配列の転送する。データの整列が乱れる)
最適化 STEP 3 23.62 GFLOPS(ホスト側から全ての配列要素を転送する)
さて、もう一つ重要なことは、前述したように、1回の命令で 16 words(これを "Superwords" と言う)をフェッチできる性能効果を有効に活かす必要があります。スレッド・ブロックの Warp の半分のスレッド(Half-Warpと言う)が、連続した16ワードを1度にレジスタに取り込めれば、GPUの持つ広いメモリバンド幅を享受できます。(Fermi すなわち Compute Capability 2.0 以降は、Warp単位である 32 words のアクセスとなります。)このためには、デバイスメモリ上に割り付けた配列データを連続してアクセスする状態を作っておく必要があります。もし、ストライドを伴うデータアクセスが想定される場合は、極力、 stride-1 の連続アクセスを行えるようにすることを考えなければなりません。このためには、プログラムを再構成する、あるいはデータのレイアウト構造を変更すると言ったことがソースプログラム上で必要になります。PGIアクセラレータコンパイラが GPUの kernel コードに翻訳する際、こうした stride-1 ではないアクセスパターンになる場合、以下のようなコンパイル・メッセージを出力します。このようなGPUコードは、ほとんど性能が向上しないと考えた方が良いでしょう。こうした状況の場合、もう一つの手は、このアクセスパターンを有する配列データを高速なキャッシュで管理すると言う方法です。
PGI Accelerator プログラミングモデルの場合のコンパイルメッセージ(-Minfo=accel) の例
32, Non-stride-1 accesses for array 'a'
③ Shared Memory を利用した明示的なキャッシュの利用
PGIアクセラレータでは、配列データのキャッシュを実装することはコンパイラ任せとなります。PGI CUDA Fortran では、ユーザのプログラミングでキャッシュ使用の実装を行います。PGIアクセラレータ・コンパイラの場合は、コンパイラがプログラムを分析して、キャッシュ化可能なものに限り自動的にキャッシュを利用できるようにします。ここで言うキャッシュとは、GPU内の Shared Memory を利用するものです。従って、そのサイズは制限があり、全てのデータがキャッシュ化できる訳ではありません。Shared Memory は、一つの SM (Streaming Multiprocessor) の中に実装され、この SM の中だけで実行する複数のスレッド・ブロックで利用されます。一つの SM 上で動作する異なるスレッドブロック数が多ければ、1スレッド・ブロックが使用できる shared memory 上で割当可能なサイズが小さくなります。従って、自ずと使用できる容量は限りがあり、そのサイズによってデータをキャッシュ化できるかどうか決まります。この姫野ベンチマーク・プログラムでも、以下のコンパイラのメッセージを見て分かるとおり、'p' 配列の隣接ポイントの値を含めて、キャッシュとして割り当てています。
Shared Memory を利用してキャッシュする最大の目的は、コアレッシング・メモリアクセスができないデータ(あるいは、non-stride-1 のメモリアクセスのデータ)をより高速にアクセスできるようにするためのものです。これによって、GPUのマルチスレッディングを向上させ、性能をより高速化することができます。
( 303) do k=2,kmax-1 ( 304) do j=2,jmax-1 ! 以下の i ループをSIMD(Vector)同期モードとすると ( 305) do i=2,imax-1 ! p(i,j,k)の隣接ポイントのアクセスは、不規則なアドレス番地のアクセス ( 306) s0=a(I,J,K,1)*p(I+1,J,K) & ! コアレッシングではない。p をキャッシュ化する。 ( 307) +a(I,J,K,2)*p(I,J+1,K) & ( 308) +a(I,J,K,3)*p(I,J,K+1) & ( 309) +b(I,J,K,1)*(p(I+1,J+1,K)-p(I+1,J-1,K) & ( 310) -p(I-1,J+1,K)+p(I-1,J-1,K)) & ( 311) +b(I,J,K,2)*(p(I,J+1,K+1)-p(I,J-1,K+1) & ( 312) -p(I,J+1,K-1)+p(I,J-1,K-1)) & ( 313) +b(I,J,K,3)*(p(I+1,J,K+1)-p(I-1,J,K+1) & ( 314) -p(I+1,J,K-1)+p(I-1,J,K-1)) & ( 315) +c(I,J,K,1)*p(I-1,J,K) & ( 316) +c(I,J,K,2)*p(I,J-1,K) & ( 317) +c(I,J,K,3)*p(I,J,K-1)+wrk1(I,J,K) ( 318) ss=(s0*a(I,J,K,4)-p(I,J,K))*bnd(I,J,K) ! a(),b(),c(),..,wrk1()等の配列のアクセスは stride-1 となる、コアレッシング ( 319) gosa= gosa + ss*ss ( 320) wrk2(I,J,K)=p(I,J,K)+OMEGA *SS ( 321) enddo ( 322) enddo ( 323) enddo 【コンパイラ・メッセージ】 305, Loop is parallelizable Accelerator kernel generated ! CUDA kernel プログラムを生成した 303, !$acc do parallel, vector(4) 304, !$acc do parallel, vector(4) ! Block=(4x4x16)のサイズ 305, !$acc do vector(16) Cached references to size [18x6x6] block of 'p'
④ Kernel のスケジューリング最適化(ブロック、グリッド構成の変更)
ユーザ自身が、PGIアクセラレータで最適化できる最も重要なカーネルスケジューリングの最適化について説明します。現在の GPU のアーキテクチャとその動作形式は、その性能の向上に線形性がありません。すなわち、GPU は、アムダール則に則ったコア数に応じて性能向上が予測できると言ったアーキテクチャではありません。プログラム内のちょっとした変更で、その性能が大幅に異なることがあります。こうしたことを NVIDIA の GPU で表現すると、CUDA kernel のスレッド・ブロックの構造や動作するグリッドの構成によって、大きく性能が変化すると言うことになります。この kernel をスケジューリングすると言うことは、最も敏感に GPU 性能を左右するものと言っても過言ではありません。しかしながら、現在のコンパイラ技術は、より良い kernel 性能スケジューリング方法を予測する知見を十分有しているとは言えません。これを代替するものとして、PGIアクセラレータコンパイラは、Kernel スケジューリングを変更するためのディレクティブをユーザに提供しています。これが、「ループマッピング・ディレクティブ」と言うものです。
Kernel スケジューリング のためのディレクティブとは、並列ループをどのように GPU ハードウェアの並列構造にマッピングさせるかと言うことをコンパイラに伝えるものです。この概念を理解することは、非常に重要です。例えば、一重の並列化可能なループがあるとします。これを並列に動作させるには、コンパイラは、ループ長をいくつかのチャンク (chunks) あるいは断片(strips) に分割し、各々並列(並行)に実行できる単位を生成します。こうした分割操作を「ストリップマイニング(strip-mine)」と呼んでいます。ここで理解して欲しいことは、「ループ長」を分割することにより、複数のチャンクが生成され、これらが独立に並列動作できるようになると言うことです。そこで、今度は、各チャンクは、GPU 上の一つの SM (Streaming Multiprocessor) 上で、SIMD あるいはベクトルモードで、自身のチャンク内の処理を実行します。「ベクトルモード」で実行させる理由は、メモリ上の Stride-1 の連続アクセス(コアレッシング)を実現させ、メモリの広帯域性能を十分に活かすためには、ハードウェア設計上、ベクトル動作(一命令で複数の演算を行える)が最も都合が良いからです。さらに、他の分割されたチャンクは、別の異なる SM を利用して、パラレルモードで実行されます。簡単に言えば、ユーザが記述したプログラムの並列ループが複数に分割され、この分割された単位がハードウェア上の一つの SM 上で動作し、複数のチャンクに分割された場合は、複数の SM 上で並列に実行されると言った形です。以上のことが、プログラム上のループ分割されたチャンクが、ハードウェア上の実行形態へマッピングされる際の状況説明となります。さて、これらの分割されたベクトルモードで実行するチャンクと言う「複数の計算要素が詰まった固まり」の番号やそのチャンク内の計算要素の番号をハードウェアは識別する必要があります。これは、CUDA環境が用意している blockidx.x や threadidx.x と言うビルトイン変数で、コンパイラが識別します。一つのチャンク内でベクトル実行する要素(実は、この各要素の実行実体は一つの CUDA スレッドにマッピングする)のインデックスを示すのが threadidx.x であり、各チャンクという「ブロック」の番号をインデックスするのが blockidx.x となります。全ての分割されたチャンク(ブロック)は一意の各インデックスを有することで、どこの誰それか?というチャンクの物理的位置と、チャンク(ブロック)内の各実行要素(各スレッド)の位置まで一意に決まります。このインデックスはユーザ・プログラムが指定したループ分割の形態に応じて、NVIDIA CUDA ソフトウェアが決めて、ハードウェアに伝えるもので、ユーザやコンパイラが blockidx.x や threadidx.x を決めるものではありません。こうしたインデックスは、ループを複数のチャンク(ブロック)に分割しなければ付番されませんので、ユーザプログラムではループ構造をどのように分割するのか、その際、ベクトルモードで実行させるループ長はどうするのかと言うことを指示する必要があります。これは、一重ループ構造だけではなく、多重ループ構造でもそれぞれのループ長を分割することができます。こうして、NVIDIA GPU上で実行する、ベクトルモードで実行するスレッド集合体のブロック(これを「スレッド・ブロック」と言う。)と、全体のループ領域の中でこのスレッド・ブロックの分割の形態(これを「グリッド」と言う。)を決めることになります。ユーザプログラム上で、「グリッド」構成が定義されることで、内部的に初めて blockidx.x や threadidx.x と言うビルトイン変数値が決定されます。
もう一つ、きちんと押さえておく必要なことがあります。「スレッド・ブロック」は、ブロック内の演算要素の実行スレッドがベクトルモードで実行するため、必ず同期処理を必要とする場面があります。GPU内部で同期処理ができるのは一つの SM (Streaming Multiprocessor) 内でしかできないため、「スレッド・ブロック」の実行は、必ず一つの SM 上だけで実行されます。 他の異なる SM 上にベクトル処理の実行中に移動して演算すると言うことはできません。一つのスレッド・ブロックには、最大 512スレッド(GT200系)、1024 スレッド(Fermi)と言うハードウェアの制約がありますので、この範囲内でいわゆるループを分割する際のベクトル長を決めなければなりません。プログラム上、ベクトルモードで実行する「ループ」とそのループ全長のうちベクトル実行する長さ(ベクトル長)を決めることにより、一意にスレッド・ブロックの形態が決定されます。多重ループ構造の場合、複数のループに対してベクトル長を指定してベクトル実行指定することもできます。この場合のスレッド・ブロックの形状は、2次元、3次元と言ったものになります。
次に、スレッド・ブロックの構造が決まれば、このブロックをどう言った形で独立並列実行させるかと言う形態を決めます。例えば、多重ループ構成の場合、それぞれのループに対して並列実行させるのか、そうでないのかと言った指示や、必要であれば明示的にグリッドのサイズの指示を行えば、CUDAのグリッド構成が決定されます。以下に、PGIアクセラレータが提供するループマッピング・ディレクティブの中の主な「ループスケジューリング・クローズ」について説明しておきます。

PGI Accelerator Loop Mapping Directives (ループマッピング・ディレクティブ)
!$acc do [clause [,clause]...]
PGI Accelerator Loop scheduling Clauses (ループスケジューリング・クローズ)
host[ (width) ]
parallel[ (width) ]
seq[ (width) ]
vector[ (width) ]
independent
kernel
private (list)
アクセラレータ計算領域内のループ構造をどのようにスレッド・ブロック化するのか、あるいは並列分割をするのかを指定するクローズ(節)です。これは、CUDAの概念で言う「ブロック」と「グリッド」の構成を指定することと同意です。まず、基本は、vector クローズと parallel クローズです。以下に主要なクローズの説明をします。
- vector クローズは、!$acc do vector の直下のループのSIMD長(ベクトル長)を指定するものです。これがCUDAで言う「スレッド・ブロック」のサイズとなります。もっと具体的に言うと、一つのブロック内で常に同じ命令で動作し、同期処理を可能とするスレッド数(threadidx に相当)を言います。このサイズは、Compute 1.3 以下は 512、Fermiで 1024 までと言う制約があります。このクローズの引数である width は、そのSIMD長を指定します。省略しても構いませんが、この場合は、コンパイラが自動指定します。複数のループに指定した場合は、その SIMD 長の積が上記の制約数を越えてはなりません。
- parallel クローズは、!$acc do parallel の直下のループを独立で並列実行することをコンパイラに指示します。一般には、width 引数を指定しなくても良いです。width 引数を指定しない場合、あるいは、並列ループ長の最大値を越える場合は、この最大値を強制的にセットします。この最大値がグリッドの一つのサイズ(blockidxに相当)となります。width 引数に値をセットするとこの値がグリッドのサイズ(blockidx)に相当し、この値が当該並列ループの最大長よりも小さい場合は、内部的にストリップマインニング(分割)されて同時に実行されます。
- host クローズは、!$acc do host の直下のループをホスト側でシーケンシャルに実行することを指示するものです。
- seq クローズは、!$acc do seq の直下のループをシーケンシャルに実行することを指示するものです。
- independent クローズは、!$acc do independent の直下のループは、並列実行の依存性がないことを明示的にコンパイラに知らせるためのものです。コンパイラが依存性有りとしたループに対しても並列化の適用を行います。このクローズは注意して使用する必要があります。
- kernel クローズは、!$acc do kernel 配下のループ群を一つの kernel としてコード生成することを指示するものです。大きな外側のループを kernel にしたい場合に便利なクローズです。
- private クローズは、!$acc do private の直下のループ内にある (list) で指定した配列、変数、部分配列が、ループ反復内で独立に使用するプライベート変数として、これらの変数のコピーを持つことを指示するものです。
さて、PGIアクセラレータのループスケジューリング・クローズの設定例をお見せし、その説明をします。以下の例は、二つのクローズ(parallel, vector)を同時に指定した場合の例です。行番号 304 ループに対して、ベクトル長256のスレッド・ブロックを作成し、全体のループ長が 256 を越えている場合は、これを256単位で分割しなさいと言う指示を与えています。さらに、分割(ストリップマイニング)されたブロックは、「並列モード」で独立に処理できることを指示しています。ハードウェアとのマッピングをしてみましょう。ベクトル長256と言うのは、1スレッド・ブロック内の「スレッド数」を意味します。このスレッド・ブロック内のスレッドは、必ず「同一の SM 」上で動作するようになります。他の分割されたスレッド・ブロックは、他の SM で並列に動作してもよいと言う意味となります。
Accelerator kernel generated
304, !$acc do parallel, vector(256)
次の例は、行番号 305 ループに対して、ベクトル長256のスレッド・ブロックを作成し、ループ長が 256 を越えている場合は、これを256単位で分割しなさいと言う指示を与えています。この分割(ストリップマイニング)されたブロックは、「シーケンシャルに実行」することを指示しています。ここが上の例とは異なります。従って、305 ループのスレッド・ブロックは全て「同一の SM 」上で順番に実行されます。そして、行番号 304 ループは、並列モードで実行することを指示しています。並列分割の単位(width) が指定されていないため、これはコンパイラに判断を任せると言う意味となります。305ループのベクトルモード実行のスレッド・ブロック単位を 304 ループの分割によって並列チャンクを生成し、これらのチャンクを並列・独立に実行すると言う形となります。
Accelerator kernel generated
304, !$acc do parallel
305, !$acc do vector(256)
次の例は、行番号 304と305 ループは、共に parallel と Vector クローズを指定しています。従って、どちらのループ共に、それぞれ4要素ずつ、すなわちベクトル長 4 x ベクトル長 4 = 16要素(スレッド)の構成となるスレッド・ブロックを形成します。スレッド・ブロックの演算を定義する CUDA kernel のプログラム内には、二重ループのコーディングがなされると考えて下さい。 (4 x 4)のスレッド・ブロックを基本単位として、これは一つの SM 上で実行されます。さらに、各ループとも 4 単位で分割された複数のチャンク(グリッドに相当)は、各々独立に任意の SM 上で並列実行されます。2次元の形状のスレッド・ブロックが二次元の形状のグリッド構成の中で、並列に実行されると言うことになります。
Accelerator kernel generated
304, !$acc do parallel, vector(4)
305, !$acc do parallel, vector(4)
次の例は、行番号 304と305 ループは、共に parallel と Vector クローズを指定しています。従って、304ループは 4 要素ずつ、すなわちベクトル長 4、305ループはベクトル長 64 の構成となり、この場合、4 x 64 = 256要素(スレッド)の構成となる 2 次元形状のスレッド・ブロックを形成します。さらに、各ループは、それぞれ 4、64 で分割した形のグリッドの構成が形成され、並列に動作することになります。なお、各ループに指定した vector (width) の width の積は、GT200 系で 512 以内、Fermiで 1024 以内であることという制約があります。
Accelerator kernel generated
304, !$acc do parallel, vector(4)
305, !$acc do parallel, vector(64)
次の例は、行番号 304 ループの外側ループが、ベクトル/並列モードで指定されています。305 内側ループは、並列モードの実行が指定されています。この指定の方法はあまりないと思いますが、例えば、外側ループのインデックスが stride-1 のアクセスになるような場合に指定します。
Accelerator kernel generated
304, !$acc do parallel, vector(256)
305, !$acc do parallel
次の例は、3重ループの設定の方法の一例です。各ループとも、4 x 4 x 16 の 3 次元ブロックを構成したベクトル実行を行う指定方法です。この 4 x 4 x 16 のブロックが、スレッド・ブロックとなります。306ループは、ベクトル実行のみの指定ですので、 4 x 4 x 16 のチャンクの単位が同一 SM 上でシーケンシャル実行されます。304と305のループは、並列実行できるように分割され、「グリッド」は 2 次元の構成となります。以下にコンパイル時のメッセージ情報とこの形態で実行したときのPGIアクセラレータ・プロファイル情報をしまします。プロファイル情報には、実行した際の kernel のグリッド形状とブロックの形状も出力されます。
Accelerator kernel generated
304, !$acc do parallel, vector(4)
305, !$acc do parallel, vector(4)
306, !$acc do vector(16)
コンパイルメッセージ(-Minfo=accel) 304, Loop is parallelizable ! ループ長 128 305, Loop is parallelizable ! ループ長 128 306, Loop is parallelizable Accelerator kernel generated 304, !$acc do parallel, vector(4) ! ループ長128/4 = 32 グリッドサイズ 305, !$acc do parallel, vector(4) ! ループ長128/4 = 32 グリッドサイズ 306, !$acc do vector(16) 実行後のアクセラレータ・プロファイル情報 Accelerator Kernel Timing data jacobi 306: kernel launched 803 times grid: [32x32] block: [16x4x4] ==> [32x32] グリッドで、[16x4x4]の形状のスレッド・ブロック time(us): total=4147281 max=5206 min=5124 avg=5164
PGIアクセラレータのループスケジューリング・クローズは、一度、試行錯誤でいろいろ変えてみて、最適となる性能を確認することをお勧めします。とは言え、お勧めのガイドラインはないのかと言うことであれば、以下をご参考にして欲しいと思います。
- 最も外側のループは、できるだけ parallel クローズで構成する。
- 多重ループ内で多くても二つのループには、parallel か parallel(width) を設定してみる。
- 最内側ループは、必ず stride-1 の連続アクセスとなるループ・インデックスとすること。
- 最内側のループには、vector(width) を設定する。そのベクトル長は、GT200系では 128~256 で、Fermi では 256 程度とする。複数のループに vector 指定しても良いが、筆者は、基本は最内側のみが良いように思っている。特に、姫野ベンチのようなメモリアクセスがインテンシブな場合は、ベクトルモード実行は、一つのループだけにすること。(これは、姫野ベンチは、メモリアクセス性能が支配する特性のため、スレッド・ブロック内で最もメモリアクセスの遅延が少ない「連続アクセス」が可能となるモードであるから)
- vector(width) の width は、CUDA Warp サイズ の 32の倍数であること。
- !$acc do parallel, vector の並列/ベクトルの同時指定を多用しないこと。まずは、シンプルな形から試すこと。最内側ループは、vector のみの指定という風に。
- -Minfo=accel で出力されるコンパイラ・メッセージの中で、「Occupancy Estimator の情報表示」があります。この中の occupancy が少なくとも 50% 以上であること。Fermi の場合は、さらに 66% 以上であることが望ましい。これは、ベクトル長の長さをある程度長くしなければならないと言うことである。
ステップ 6 (ループスケジューリングの最適化)
GTX 480 (Fermi) 上での実行
姫野ベンチマークのPGIアクセラレータによる性能最適化の最終ステップです。上記で述べたループスケジューリングの最適化を実施した結果を以下に示します。ここでは、ループスケジューリング・クローズの最適値の試行錯誤についてはコメントしません。これは、経験を一度しなければ実感がわかないと言うのが正直なところで、是非、試行錯誤してみて下さい。なお、以下の kernel スケジューリングでは、GTX 285 (CC 1.3)の GPU で実行すると、17 GFLOPS 程度となり遅くなってしまいます。(GTX285上の性能は、後述します)
( 300) !$acc copyin (a(1:mimax,1:mjmax,1:mkmax,1:4)) & ( 301) !$acc copyin (b(1:mimax,1:mjmax,1:mkmax,1:3), c(1:mimax,1:mjmax,1:mkmax,1:3)) & ( 302) !$acc copy (p(1:mimax,1:mjmax,1:mkmax)) & ( 303) !$acc copyin (wrk1(1:mimax,1:mjmax,1:mkmax), bnd(1:mimax,1:mjmax,1:mkmax)) & ( 304) !$acc local (wrk2(1:mimax,1:mjmax,1:mkmax)) ( 305) ( 306) !$acc region copyin(omega),copy(gosa),local(ss,s0) ( 307) !$acc do host ( 308) do loop=1,nn ( 309) gosa = 0.0 ( 310) ( 311) !$acc do parallel(16) ( 312) do k=2,kmax-1 ( 313) !$acc do parallel ( 314) do j=2,jmax-1 ( 315) !$acc do vector(256) ( 316) do i=2,imax-1 ( 317) s0=a(I,J,K,1)*p(I+1,J,K) & ( 318) +a(I,J,K,2)*p(I,J+1,K) & ( 319) +a(I,J,K,3)*p(I,J,K+1) & ( 320) +b(I,J,K,1)*(p(I+1,J+1,K)-p(I+1,J-1,K) & ( 321) -p(I-1,J+1,K)+p(I-1,J-1,K)) & ( 322) +b(I,J,K,2)*(p(I,J+1,K+1)-p(I,J-1,K+1) & ( 323) -p(I,J+1,K-1)+p(I,J-1,K-1)) & ( 324) +b(I,J,K,3)*(p(I+1,J,K+1)-p(I-1,J,K+1) & ( 325) -p(I+1,J,K-1)+p(I-1,J,K-1)) & ( 326) +c(I,J,K,1)*p(I-1,J,K) & ( 327) +c(I,J,K,2)*p(I,J-1,K) & ( 328) +c(I,J,K,3)*p(I,J,K-1)+wrk1(I,J,K) ( 329) ss=(s0*a(I,J,K,4)-p(I,J,K))*bnd(I,J,K) ( 330) gosa= gosa + ss*ss ( 331) wrk2(I,J,K)=p(I,J,K)+OMEGA *SS ( 332) enddo ( 333) enddo ( 334) enddo ( 335) ( 336) ! p(2:imax-1,2:jmax-1,2:kmax-1)= & ( 337) ! wrk2(2:imax-1,2:jmax-1,2:kmax-1) ( 338) ( 339) !$acc do parallel(8) ( 340) do k=2,kmax-1 ( 341) !$acc do parallel ( 342) do j=2,jmax-1 ( 343) !$acc do vector(256) ( 344) do i=2,imax-1 ( 345) p(I,J,K)=wrk2(I,J,K) ( 346) enddo ( 347) enddo ( 348) enddo ( 349) ( 350) enddo ( 351) !$acc end region ( 352) !$acc end data region
上記のソースに対するコンパイルメッセージです。リストの中の「Occupancy Estimator の情報表示」も見て下さい。
● Fermi GPUに対する最適化 [kato@photon29 STEPS]$ pgfortran -V pgfortran 10.6-0 64-bit target on x86-64 Linux -tp nehalem-64 [kato@photon29 STEPS]$ make step6.exe (略) ! 行番号312~316 ループまで並列化可能 312, Loop is parallelizable 314, Loop is parallelizable 316, Loop is parallelizable Accelerator kernel generated 312, !$acc do parallel(16) ==> [16x..] グリッド Cached references to size [258x3x3] block of 'p' 314, !$acc do parallel 316, !$acc do vector(256) ==> [256] ベクトルモードのみ CC 1.0 : 18 registers; 9320 shared, 172 constant, 0 local memory bytes; 33 occupancy CC 1.3 : 18 registers; 9320 shared, 172 constant, 0 local memory bytes; 25 occupancy CC 2.0 : 23 registers; 9296 shared, 188 constant, 0 local memory bytes; 83 occupancy 340, Loop is parallelizable 上記の CC2.0 の occupancy 83% 342, Loop is parallelizable 344, Loop is parallelizable Accelerator kernel generated 330, Sum reduction generated for gosa 340, !$acc do parallel(8) 342, !$acc do parallel 344, !$acc do vector(256) CC 1.0 : 11 registers; 28 shared, 152 constant, 0 local memory bytes; 66 occupancy CC 1.3 : 11 registers; 28 shared, 152 constant, 0 local memory bytes; 100 occupancy CC 2.0 : 13 registers; 8 shared, 184 constant, 0 local memory bytes; 100 occupancy
以下に、実行結果を示しました。実行性能は、46.2 GFLOPS に一気に向上しました。
●GTX480(Fermi)上での実行結果
[kato@photon29 STEPS]$ step6.exe
For example:
Grid-size=
XS (64x32x32)
S (128x64x64)
M (256x128x128)
L (512x256x256)
XL (1024x512x512)
Grid-size =
mimax= 257 mjmax= 129 mkmax= 129
imax= 256 jmax= 128 kmax= 128
Time measurement accuracy : .10000E-05
Start rehearsal measurement process.
Measure the performance in 3 times.
initialize nvidia GPU
MFLOPS: 7221.508 time(s): 5.6957000000000001E-002 1.6939555E-03
Now, start the actual measurement process.
The loop will be excuted in 800 times.
This will take about one minute.
Wait for a while.
Loop executed for 800 times
Gosa : 8.3822053E-04
MFLOPS: 46177.80 time(s): 2.375256000000000
Score based on Pentium III 600MHz : 557.4337
Accelerator Kernel Timing data
/home/kato/GPGPU/Himeno/STEPS/step6.F90
jacobi
306: region entered 2 times
time(us): total=2336318 init=1 region=2336317
kernels=2290007 data=0
w/o init: total=2336317 max=2327360 min=8957 avg=1168158
316: kernel launched 803 times
!grid: [16x126] block: [256]
time(us): total=2021881 max=2555 min=2499 avg=2517
330: kernel launched 803 times
grid: [1] block: [256]
time(us): total=8909 max=12 min=11 avg=11
344: kernel launched 803 times
grid: [8x126] block: [256]
time(us): total=259217 max=328 min=320 avg=322
/home/kato/GPGPU/Himeno/STEPS/step6.F90
jacobi
299: region entered 2 times
time(us): total=2432207
data=85606
acc_init.c
acc_init
41: region entered 1 time
time(us): init=570835
GTX 285 上での実行
GTX 285 (CC 1.3)の場合は、コンパイラが自動で設定した parallel/vector クローズの値が最適性能となりました。(PGI 10.6の場合)
( 311) !$acc do parallel, vector(4) ! GTX480とは異なる ( 312) do k=2,kmax-1 ( 313) !$acc do parallel, vector(4) ! GTX480とは異なる ( 314) do j=2,jmax-1 ( 315) !$acc do vector(16) ! GTX480とは異なる ( 316) do i=2,imax-1 ( 317) s0=a(I,J,K,1)*p(I+1,J,K) & ( 318) +a(I,J,K,2)*p(I,J+1,K) & ( 319) +a(I,J,K,3)*p(I,J,K+1) & ( 320) +b(I,J,K,1)*(p(I+1,J+1,K)-p(I+1,J-1,K) & ( 321) -p(I-1,J+1,K)+p(I-1,J-1,K)) & ( 322) +b(I,J,K,2)*(p(I,J+1,K+1)-p(I,J-1,K+1) & ( 323) -p(I,J+1,K-1)+p(I,J-1,K-1)) & ( 324) +b(I,J,K,3)*(p(I+1,J,K+1)-p(I-1,J,K+1) & ( 325) -p(I+1,J,K-1)+p(I-1,J,K-1)) & ( 326) +c(I,J,K,1)*p(I-1,J,K) & ( 327) +c(I,J,K,2)*p(I,J-1,K) & ( 328) +c(I,J,K,3)*p(I,J,K-1)+wrk1(I,J,K) ( 329) ss=(s0*a(I,J,K,4)-p(I,J,K))*bnd(I,J,K) ( 330) gosa= gosa + ss*ss ( 331) wrk2(I,J,K)=p(I,J,K)+OMEGA *SS ( 332) enddo ( 333) enddo ---------------------------------------- Now, start the actual measurement process. The loop will be excuted in 800 times. This will take about one minute. Wait for a while. Loop executed for 800 times Gosa : 8.3709299E-04 MFLOPS: 23683.30 time(s): 4.631285000000000 Score based on Pentium III 600MHz : 285.8921 Accelerator Kernel Timing data /home/kato/GPGPU/Himeno/STEPS/step62.F90 jacobi 306: region entered 2 times time(us): total=4603216 kernels=4552682 data=0 316: kernel launched 803 times grid: [32x32] block: [16x4x4] time(us): total=4134008 max=5388 min=4967 avg=5148 330: kernel launched 803 times grid: [1] block: [256] time(us): total=9484 max=16 min=11 avg=11 344: kernel launched 803 times grid: [8x126] block: [256] time(us): total=409190 max=536 min=489 avg=509
ステップ 7 (データ整列の最適化)
128バイト境界のデータ・アラインメントの適用
最後に、上記の「① 配列データのアラインメント」の項の説明にあった、データ境界のアラインメント(整列)を行った場合の性能を測定してましょう。私が提供したソースファイルのアーカイブの中に、padding.F90 (Fermi対応)と言うファイルが、その最適化を施したものとなります。step 6 のソースに、データのアライメント調整を施しました。Fermi 以外の CC 1.3 以前の GPU 用は、padding2.F90 と言うファイルを使用して下さい。GTX480(Fermi) での実行結果は以下の通りです。
●GTX480(Fermi)上での実行結果
[kato@photon29 STEPS]$ padding.exe
mimax= 288 mjmax= 129 mkmax= 129
imax= 256 jmax= 128 kmax= 128
Time measurement accuracy : .10000E-05
Start rehearsal measurement process.
Measure the performance in 3 times.
initialize nvidia GPU
MFLOPS: 6623.757 time(s): 6.2096999999999999E-002 1.6939555E-03
Now, start the actual measurement process.
The loop will be excuted in 800 times.
This will take about one minute.
Wait for a while.
Loop executed for 800 times
Gosa : 8.3822053E-04
MFLOPS: 47120.96 time(s): 2.327714000000000
Score based on Pentium III 600MHz : 568.8189
姫野ベンチマークの各作業ステップの性能(総括)
さて、今までの各最適化ステップの性能を整理しておきましょう。最適化と言っても、単なるディレクティブの挿入とその kernel ループスケジューリングの調整だけです。結果だけ見れば、何だこんなものか!と言う程度の作業です。
PGIアクセラレータプログラミングモデルによる最初の最適化作業フェーズにおける性能は以下の通りです。GTX480(Fermi) と GTX 285 の性能を示しました。なお、以下の表は PGI 10.6 バージョンを使用した際の性能です。
| 作業(最適化)ステップ | GTX 480 | GTX 285 | |
|---|---|---|---|
| STEP 1 | 反復ループの内側にアクセラレータ計算領域ディレクティブ | 1.29 GFLOPS | 1.27 GFLOPS |
| STEP 2 | 反復ループの外側にアクセラレータ計算領域ディレクティブ | 24.20 GFLOPS | 18.29 GFLOPS |
| STEP 3 | STEP 2+データ転送Clauseを追加指定 | 24.41 GFLOPS | 23.62 GFLOPS |
| STEP 4 | 反復ループの内側にアクセラレータ計算領域を置き、別途、データ領域ディレクティブ使用 | 24.33 GFLOPS | 23.54 GFLOPS |
| STEP 5 | STEP 3+データ領域ディレクティブを別途指定 | 24.40 GFLOPS | 23.68 GFLOPS |
| STEP 6 | Kernel のスケジューリング最適化 (GTX480と285では異なる方法でチューニング) | 46.17 GFLOPS | 23.63 GFLOPS |
| STEP 7 | STEP 6 + 配列データのアラインメント(整列)調整 | 47.12 GFLOPS | 24.60 GFLOPS |
さて、参考のためもう一つの性能を示さなければなりません。これは、PGI 10.4 を使用した場合の性能です。PGI Accelerator Compiler は、そのアクセラレータ機能に関しては発展途上です。従って、毎月リリースされる各リビジョンで、同じプログラムでありながらその性能が変化しています。PGIアクセラレータ機能の中核となる機能として Planner と言うコンポーネントがあります。これは、プログラムの「ループ・パラレリズム」とハードウェアの「デバイス・パラレリズム」をマッピングする機能ですが、ちょうど本稿で説明したループスケジューリングの調整や、メモリアクセスのパターンを最適にすると言った様々な機能です。現在、この機能向上のために、毎リビジョン変化しています。その副作用として、以前のリビジョンより PGI 10.6 は性能が低下していている現象が見られます。(GPUコードの中身を見ましたが、以前のバージョンと較べ大きく異なっております。)ただ、これは性能向上のための途上における副作用ですので、今後のPGIコンパイラのリビジョンに期待していただきたいと思います。そこで、PGI 10.4 で実行した結果を以下に纏めます。
| 作業(最適化)ステップ | GTX 480 | GTX 285 | |
|---|---|---|---|
| STEP 3 | STEP 2+データ転送Clauseを追加指定 | 24.72 GFLOPS | 23.49 GFLOPS |
| STEP 4 | 反復ループの内側にアクセラレータ計算領域を置き、別途、データ領域ディレクティブ使用 | 24.62 GFLOPS | 23.39 GFLOPS |
| STEP 5 | STEP 3+データ領域ディレクティブを別途指定 | 24.70 GFLOPS | 23.48 GFLOPS |
| STEP 6 | Kernel のスケジューリング最適化 | 53.13 GFLOPS | 23.77 GFLOPS |
| STEP 7 | STEP 6 + 配列データのアラインメント(整列)調整 | 55.78 GFLOPS | 25.38 GFLOPS |
※STEP 7 の GTX285 上の測定に用いたPGI10.4バイナリは、padding2.exe ではなく、padding.exe です。PGI10.4 の場合は、こちらの方が性能が高い。
●PGIアクセラレータによる姫野ベンチマークの最適化手順 コラム(全2回)
- その 1 :単純に簡単なPGIアクセラレータ用ディレクティブだけを適用
- その 2 :PGIアクセラレータの kernel ループスケジューリングの最適化の適用(本稿)
