[cuSOLVER]LAPACKライブラリを使ったアプリケーションのGPU高速化
目次
はじめに
プロメテックの阿部です。HPCエンジニアとして、プログラムのGPU高速化の業務を担当しています。このコラムは、
- LAPACKライブラリを使ったアプリケーションのGPU化の方法を、LU分解を使って連立方程式を解く例を通して知る。
- アプリケーション性能のCPUとGPUの比較を行い、GPUを数値計算に用いる利点と課題を知る。
を目的としています。今回のコラムは、アプリケーションのGPU化により、どのくらい性能向上するか知りたい方や、LAPACKライブラリを使ったアプリケーションを高速化したい方(そのためのGPU化の方法を知りたい方)に参考になればと思います。今回の記事の執筆にあたり、PGIコンパイラの記事を参考にしました。今回は、NVIDIA HPC SDKを用いてCPUとGPUの実行時間の比較を行いました。
今回評価したCPUとGPU
今回評価したCPUとGPUを表1に示します。
| 製品名 | 理論演算性能 (倍精度浮動小数点演算) |
Clock rate [GHz] |
Memory [GiB] |
core | CUDA version | |
| CPU | Intel(R) Xeon(R) W-2123 CPU | 460.8 GFLOPS | 3.60 | 64 | 4 | |
| GPU | NVIDIA Quadro GV100 (Volta) | 7.4 TFLOPS | 1.627 | 32 | CUDA Cores: 5,120 Tensor Cores: 640 |
11.7 |
今回評価したアプリケーションの概要
今回は、LU分解(A=LU)を使って連立方程式(Ax=b)を解くプログラムを評価しました。私は、大学院生の時に量子多体問題の研究を行い、角運動量射影法により量子系の回転エネルギーを計算する際にLU分解を使いました。プログラムでは、LAPACKライブラリとしてDgetrfとDgetrs(以下、2つ合わせて“Dgetrf(s)’’などと略す)を使いました。また、それらのLAPACKライブラリを使ったプログラムを、cuSolverライブラリを使ってGPU化しました。Dgetrf(s)に対応するcuSolverライブラリは、cuSolverDnDgetrf(s)です。
| LAPACK | cuSolver | |
| LU分解 | Dgetrf | cuSolverDnDgetrf |
| 連立方程式 | Dgetrs | cuSolverDnDgetrs |
アプリケーション性能のCPUとGPUの比較
まず、実行時間の測定結果を先にお見せします。プログラムをGPU化する具体的な方法や性能の詳細は後で説明します。
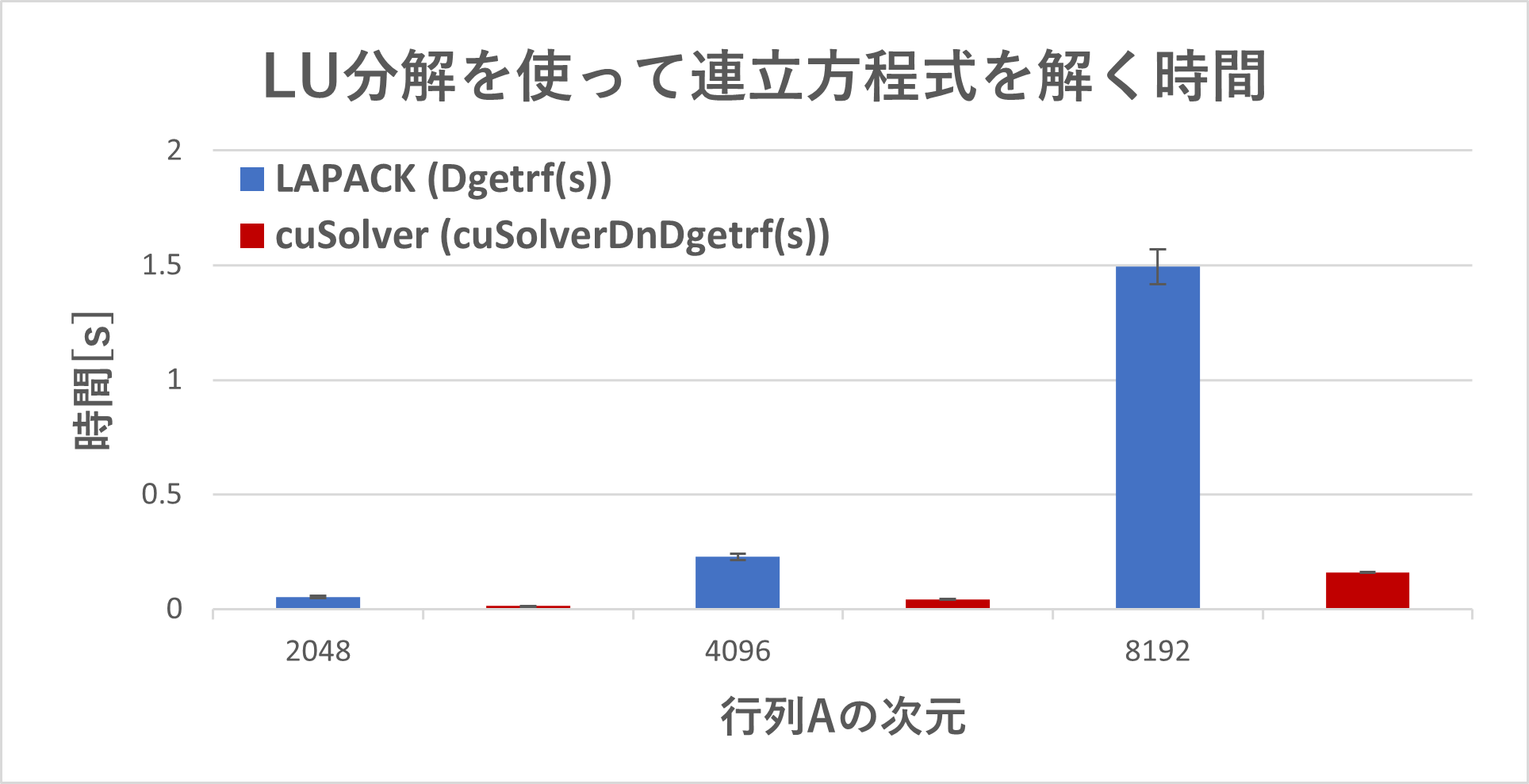
CPUとGPU上でのLU分解を使って連立方程式を解く時間を図1に示しました。行列の次元が大きくなると、CPUと比べてGPU上での実行時間は大きく減少し、行列の次元が8192の場合には9.3倍性能が向上しました。GPU化に伴うoverheadを考慮した結果の詳細については後ほどお見せします。
LAPACKライブラリ(LU分解)を使ったアプリケーションをGPU用に書き換える方法
LAPACKライブラリを使ったアプリケーションをGPU用に書き換える方法についてご説明します。今回、新たにLU分解を使って連立方程式を解くプログラムを作成しました。ソースコードは以下から取得できます。
| ライブラリ | ソースコード名 |
| LAPACK | dgetrs_lapack.f90 |
| cuSolver | dgetrs_cusolver.f90 |
以下は、CPU上でLAPACKライブラリを使って解くプログラムのソースコードの一部を抜粋したものです。(左の数字は行番号です。)
(前略)
23 integer, parameter :: m = 5 ! row number of matrix A
24 integer, parameter :: n = m ! column number of matrix A
25 integer, parameter :: nrhs = 2 ! number of vector b
26 integer, parameter :: lda = m
27 integer, parameter :: ldb = n
29 integer :: i, j, k, min_mn
30 real(8) :: a(lda, n) ! m x m matrix A
31 real(8) :: b(ldb, nrhs) ! n x nrhs RHS (set of vectors b)
43 ! LAPACK
44 integer, allocatable :: ipiv(:)
45 integer :: info_f, info_s
(中略)
134 min_mn = min(m, n) ! mとnの小さい方をmin_mnに代入
135 allocate (ipiv(min_mn)) ! allocateにより、配列ipivの次元をここで定義
139 ! LU factorization
140 call Dgetrf(m, n, a, lda, ipiv, info_f)
141 ! solve simultaneous equation
142 ! 'N': non-transpose of the matrix A
143 call Dgetrs('N', n, nrhs, a, lda, ipiv, b, ldb, info_s)
(後略)
|
140行目でLAPACKライブラリのDgetrfにより行列AはLU分解され、143行目でDgetrsにより連立方程式Ax=bの解xを計算しています。変数m(=n)は行列Aの次元、nrhsはベクトルbの個数です。変数ipivはピボット行列を表す一次元の配列です。以下は、行列Aが5×5行列の場合のコンパイルと実行結果の例です。
(CPU上でのコンパイル・実行結果)
[abe@gv100-ws ~]$ nvfortran -fast -lblas -llapack dgetrs_lapack.f90 -o dgetrs_lapack
[abe@gv100-ws ~]$ ./dgetrs_lapack
Dgetrs (LAPACK)
Time measurement accuracy : .10000E-05
lda,ldb 5 5
A=LU
generate b
Matrix A
1.00 1.12 0.90 0.62 0.31
1.12 2.25 2.18 1.59 0.93
0.90 2.18 3.19 2.73 1.78
0.62 1.59 2.73 3.44 2.57
0.31 0.93 1.78 2.57 3.00
RHS
0.41 0.51
0.69 0.79
0.91 1.01
1.05 1.15
1.10 1.20
time: 5.0900000000000001E-004 sec
LU factorization
1.12 2.25 2.18 1.59 0.93
0.89 -0.89 -1.05 -0.80 -0.53
0.55 -0.38 1.12 2.25 1.86
0.80 -0.42 0.89 -0.89 -0.85
0.28 -0.35 0.72 -0.25 1.00
Solution
0.271E+00 0.396E+00
0.203E-01 -0.120E-01
0.365E-01 0.455E-01
-0.393E-01 -0.516E-01
0.344E+00 0.380E+00
det(A): 1.000000000000001
|
このプログラムでは、はじめに適当な上三角行列Uと下三角行列Lを用意し、A=LUによって正則行列Aを計算しました。行列Aをdet(A)=1を満たすように用意したため、行列の次元が大きくなっても連立方程式の解が比較的安定して得られました。
このLAPACKを使って連立方程式を解くプログラムを、OpenACCのディレクティブを挿入することによりGPU化しました。この作業時間は2時間ほどかかりました。今回は、cuSolverを使うことで比較的容易にGPU上で実行することができました。CPU上でLAPACKを使って連立方程式を解く方法と、GPU上でcuSolverを使って連立方程式を解く方法の大まかな流れを図2で比較しました。
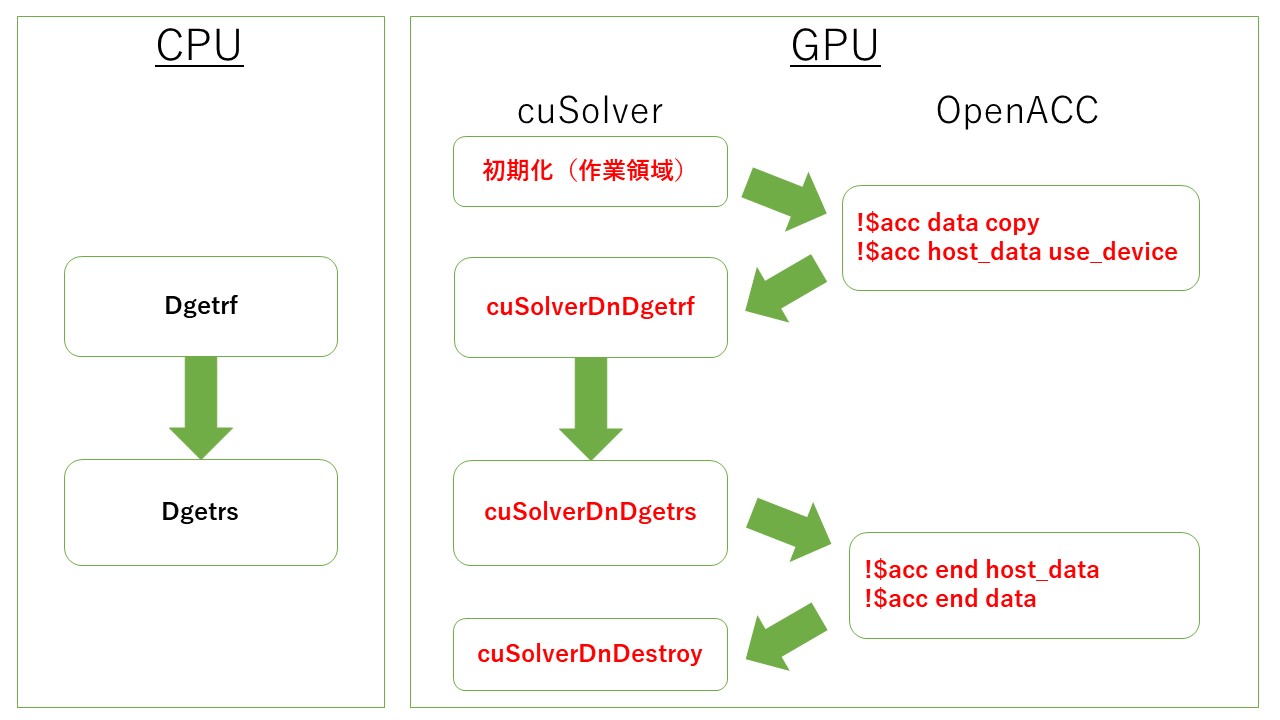
図2 CPU上でLAPACKを使うプログラムのGPU化。
cuSolverライブラリのcuSolverDnDgetrf(s)は、LAPACKライブラリのDgetr(s)に対応します。cuSolverを使うためには、GPUの作業領域の初期化をする必要があります。以下はGPU化したプログラムの一部です。
(前略)
22 use cuBlas_v2 ! cudaでLAPACKを使う場合に追加
23 use cuSolverDn ! cudaで密行列に対するLAPACKライブラリを使う場合に追加
45 ! cuSolver
46 type(cuSolverDnHandle) :: h ! h: handle
47 integer :: istat, istat_f, istat_s
48 integer, allocatable :: devIpiv(:)
49 integer :: devInfo_d
50 real(8), allocatable :: workspace_d(:)
51 integer :: Lwork
(中略)
143 cpu0 = second() ! 時間の計測
144
145 ! prior to calling any other library function
146 istat = cuSolverDnCreate(h)
150 cpu1 = second() ! 時間の計測
151
152 !$acc data copy(a, b) copyout(devIpiv, devInfo_d)
153
154 !$acc host_data use_device(a)
155 ! buffer size
156 istat = cuSolverDnDgetrf_bufferSize(h, m, n, a, lda, Lwork)
157 !$acc end host_data
161 allocate (workspace_d(Lwork)) ! executed on CPU
162 !$acc enter data create(workspace_d)
163
164 !$acc host_data use_device(a, b, workspace_d, devIpiv, devInfo_d)
165
166 cpu2 = second() ! 時間の計測
167
168 ! LU factorization
169 istat_f = cuSolverDnDgetrf(h, m, n, a, lda, workspace_d, devIpiv, devInfo_d)
170 ! solve simultaneous equation
171 ! 'CUBLAS_OP_N': non-transpose of the matrix A
172 istat_s = cuSolverDnDgetrs(h, CUBLAS_OP_N, n, nrhs, a, lda, devIpiv, b, ldb, devInfo_d)
173
174 cpu3 = second() ! 時間の計測
175
176 !$acc end host_data
177
178 !$acc exit data delete(workspace_d)
179
180 !$acc end data
181
182 ! destroy handle
183 istat = cuSolverDnDestroy(h)
187 cpu4 = second() ! 時間の計測
(後略)
|
プログラムのGPU化に伴う主な変更点は、
です。以下は、行列Aが5×5行列の場合のプログラムのコンパイルとプロファイリングツールnvprofを用いた実行結果です。
(GPU上でのコンパイル・実行結果)
[abe@gv100-ws ~]$ module load nvhpc/22.5
[abe@gv100-ws ~]$ nvfortran -acc -fast -target=gpu -Mcudalib=cublas,cusolver dgetrs_cusolver.f90 -o dgetrs_cusolver
[abe@gv100-ws ~]$ nvprof ./dgetrs_cusolver
abe@gv100-ws lapack_cusolver_gpu]$ nvprof ./dgetrs_cusolver
Dgetrs (cuSolver)
Time measurement accuracy : .10000E-05
lda,ldb 5 5
A=LU
generate b
Matrix A
1.00 1.12 0.90 0.62 0.31
1.12 2.25 2.18 1.59 0.93
0.90 2.18 3.19 2.73 1.78
0.62 1.59 2.73 3.44 2.57
0.31 0.93 1.78 2.57 3.00
RHS
0.41 0.51
0.69 0.79
0.91 1.01
1.05 1.15
1.10 1.20
==78999== NVPROF is profiling process 78999, command: ./dgetrs_cusolver
0-1 time:
0.7571530000000000 sec
1-2 time:
1.6590000000000001E-002 sec
2-3 time:
1.2500000000000000E-004 sec
3-4 time:
1.2519999999999999E-003 sec
0-4 time:
0.7751199999999999 sec
LU factorization
1.12 2.25 2.18 1.59 0.93
0.89 -0.89 -1.05 -0.80 -0.53
0.55 -0.38 1.12 2.25 1.86
0.80 -0.42 0.89 -0.89 -0.85
0.28 -0.35 0.72 -0.25 1.00
Solution
0.271E+00 0.396E+00
0.203E-01 -0.120E-01
0.365E-01 0.455E-01
-0.393E-01 -0.516E-01
0.344E+00 0.380E+00
det(A): 1.000000000000001
==78999== Profiling application: ./dgetrs_cusolver
==78999== Profiling result:
Type Time(%) Time Calls Avg Min Max Name
GPU activities: 19.80% 14.335us 1 14.335us 14.335us 14.335us void trsm_ln_kernel<double, unsigned int=32, unsigned int=32, unsigned int=4, bool=1>(int, int, double const *, int, double*, int, double, double const *, int, int*)
19.67% 14.240us 1 14.240us 14.240us 14.240us void trsm_ln_up_kernel<double, unsigned int=32, unsigned int=32, unsigned int=4, bool=0>(int, int, double const *, int, double*, int, double, double const *, int, int*)
17.33% 12.544us 1 12.544us 12.544us 12.544us void getf2_cta_32x32<double, double>(int, int, int, int, double*, int, int*, int*)
8.36% 6.0480us 4 1.5120us 1.3120us 2.0480us [CUDA memcpy DtoH]
7.03% 5.0880us 1 5.0880us 5.0880us 5.0880us void laswp_kernel2<double, bool=0, int>(int, double*, unsigned long, int, int, int const *, int)
5.57% 4.0320us 1 4.0320us 4.0320us 4.0320us getrf2_set_info(int, int, int, int*)
5.08% 3.6800us 1 3.6800us 3.6800us 3.6800us dtrsv_init(int*)
4.51% 3.2640us 1 3.2640us 3.2640us 3.2640us getrf2_reset_info(int*)
4.24% 3.0720us 1 3.0720us 3.0720us 3.0720us copy_info_kernel(int, int*)
4.24% 3.0720us 1 3.0720us 3.0720us 3.0720us dtrsv_init_up(int*, int)
4.16% 3.0080us 2 1.5040us 1.1840us 1.8240us [CUDA memcpy HtoD]
API calls: 85.70% 543.46ms 18 30.192ms 538ns 294.22ms cudaFree
11.48% 72.801ms 3 24.267ms 2.9160us 72.795ms cudaStreamCreateWithFlags
2.37% 15.004ms 1 15.004ms 15.004ms 15.004ms cuMemHostAlloc
OpenACC (excl): 98.80% 15.145ms 1 15.145ms 15.145ms 15.145ms acc_enter_data@dgetrs_cusolver.f90:152
(1%未満のものは省略)
|
今回のアプリケーションで行列の次元が小さい場合は、cudaFree等のGPU作業領域初期化処理のoverheadが顕著になり、かえって実行時間が増えてしまいました。
アプリケーション性能のCPUとGPUの比較の詳細
最後に、GPU化に伴うoverheadを含めた測定結果の詳細をお見せします。
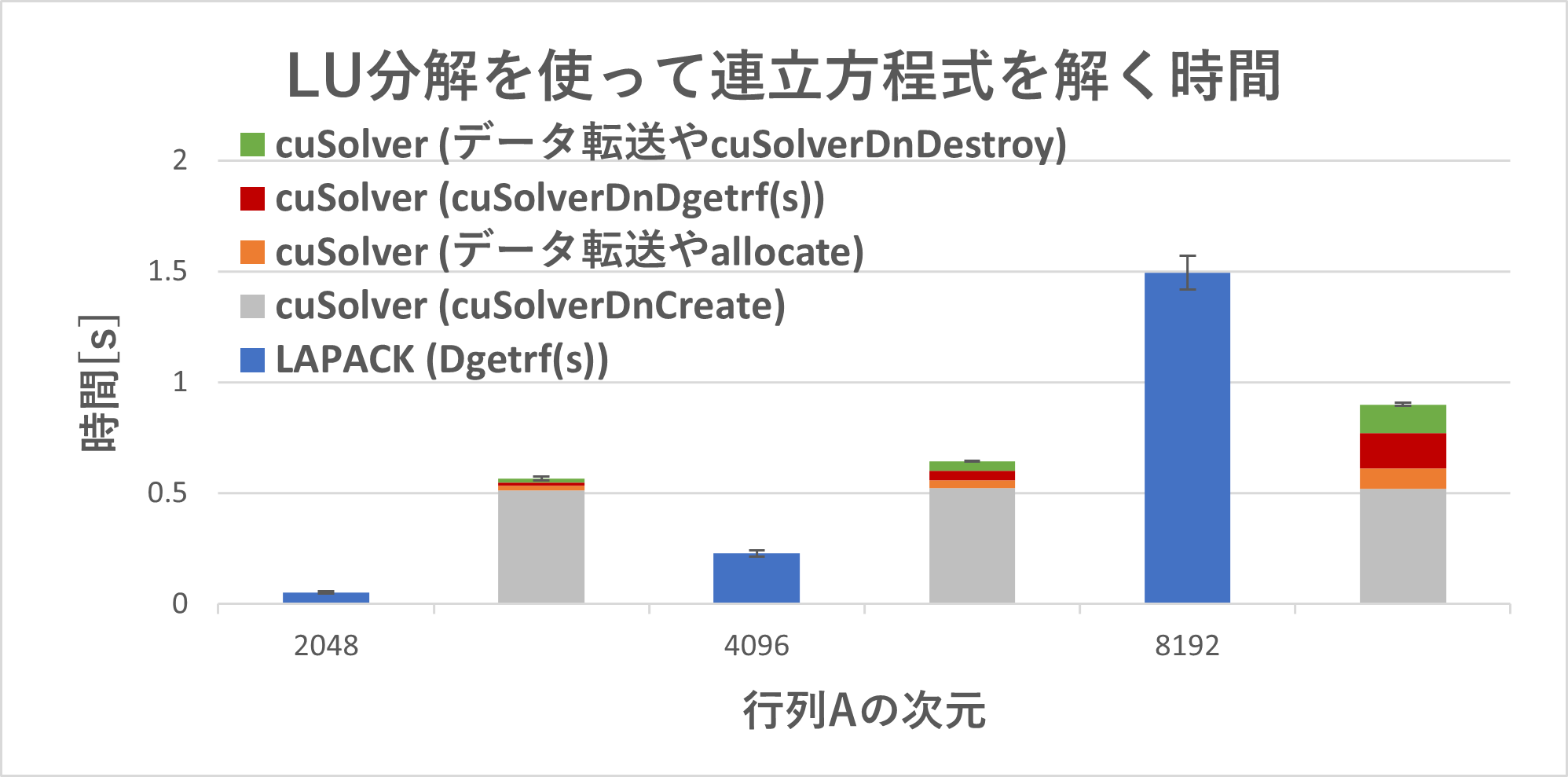
図3 CPUとGPU上で、LU分解を使って連立方程式を解く時間。LAPACK (Dgetrf(s))(青)はDgetr(s)(GPU化する前のプログラムの140行目から143行目まで)の実行時間。cuSolver (cuSolverDnCreate)(グレー)はGPU化した後のプログラムの143行目から150行目、(データ転送やallocate)(橙)は150行目から166行目、(cuSolverDnDgetrf(s))(赤)は166行目から174行目、(データ転送やcuSolverDnDestroy)(緑)は174行目から187行目の実行時間。
図3は、図1の結果にcuSolverを使うためのoverheadを含めたものです。実行時間の測定をそれぞれ5回ずつ行い、平均値と標準偏差を計算しました。GPU化した後のプログラムの実行時間については、全体だけでなく重要な部分を分けて測定しました。行列Aの次元を大きくするとCPUに対するGPUの性能が向上し、行列の次元が8192の場合には1.6倍性能が向上しました。また、GPUはCPUと比べて、実行時間の測定誤差が小さく、行列の次元が8192の場合には10倍安定していることもわかりました。GPUの作業領域の初期化で必要なcuSolverDnCreateは約0.52秒かかり、この影響は無視できませんが、この時間は行列Aの次元にはあまり依りませんでした。cuSolverDnCreateは一度のみ呼び出せばよいことや、データ転送のコストは減らす余地があることも考慮すると、LAPACKライブラリを使ったアプリケーションのGPU高速化は、アプリケーションによって変わるものと捉えるのがフェアだと思いました。
まとめ
今回は、Lapackライブラリ(LU分解)を使ったアプリケーションのGPU高速化をしてみました。そのプログラムを用いて、アプリケーションの実行時間の測定を行い、アプリケーション性能のCPUとGPUの比較を行いました。計算量が大きくなるとCPUに対するGPUの性能が向上し、1.6倍の性能向上ができました。GPUを用いることにより、LU分解を使って連立方程式を解く時間は短縮できる一方、行列の次元が小さい場合はGPUメモリ管理コスト等によるoverheadが無視できない課題があることもわかり、今後検討していきたいと思います。

