[cuSPARSE-GPUライブラリ]cuSPARSE を使用した 共役勾配法(CG)プログラム
目次
はじめに
プロメテックの星屋です。以前 阿部さんが LAPACKライブラリを使ったアプリケーションのGPU高速化 のコラムでcuSOLVERライブラリを利用した記事を執筆していますが、今回 cuSPARSEライブラリを利用して 連立一次方程式をGPUで解いてみました。
今回の記事では
- cuSPARSE(cuBLAS)ライブラリをOpenACCを使用して共役勾配法(Conjugate Gradient=CG)を実装し 利用する(cudaを使わずに) 。
- 実装した共役勾配法サブルーチンを流体シミュレーション(CFD)に利用して、CPUとの性能比較を行う
について紹介します。
なお、本内容は GPUプログラミング勉強会 で詳細を紹介させて頂いています(次回9/8金)。
今回のコラムは、BLASライブラリやIntel MKL(Math Kernel Library)を利用している方がアプリケーションをGPU化したり、流体シミュレーションを利用されている方がGPU計算の効果を知りたい方の参考になればと思います。
(備考)HPC WORLDのアーカイブには cuSPARSE/OpenACC を利用した線形方程式の反復解法プログラム という記事がありますが、現状のHPC SDKではこのプログラムがコンパイルできないようです。今回この記事を参考に一部 行列ベクトル積について cusparseSpMV を使って実装しました。
連立一次方程式の解法(共役勾配法=Conjugate Gradient)
構造解析や流体解析で用いられる 有限要素法(FEM)や有限体積法(FVM)では、連立一次方程式を解くことが重要であり、共役勾配法=Conjugate Gradient(CG)に代表される陰解法が良く用いられています。
一次方程式の係数行列をA, 右辺ベクトルをb として、Ax=bの解 Xを以下のアルゴリズムで反復計算により求めます。
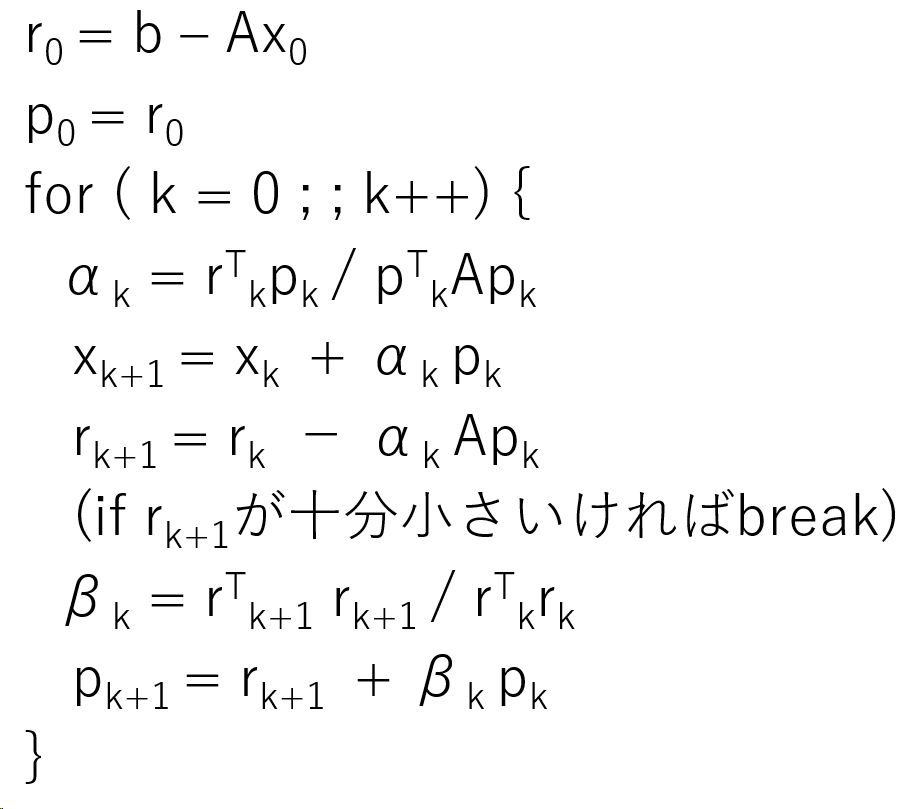
上記で ベクトルの計算や内積に cuBLAS を利用し、行列ベクトル積に cuSPARSEを利用しました。
cuSPARSEを利用した共役勾配法(CG)の実装
HPC WORLDのアーカイブでは、CG/ICLU/ICCL を cuBLAS/cuSPARSEを利用してGPUで実行する例が記載されていますが、このソースコードを流用させていただき、CG部分のみをcuSPARSEで再実装してみました(行列ベクトル積以外はオリジナルのcuBLASを利用したコードをそのまま利用しています)。
ソースコード(cg_cuspase.f90)は こちら
NVIDIA HPC SDKのFortranコンパイラでコンパイルします。
cuBLAS, cuSPARSEを利用するためにコンパイルオプション’-cudalib=cublas,cusparse’ を指定します。
$ nvfortran cg_cusparse.f90 -cudalib=cublas,cusparse -acc -Minfo=accel -O2
cg:
274, Generating create(q(:)) [if not already present]
Generating copy(r(:)) [if not already present]
Generating copyin(csrrowptra(:),csrcolinda(:),csrvala(:)) [if not already present]
Generating create(p(:)) [if not already present]
Generating copy(x(:)) [if not already present]
304, Generating create(buffermv(1:buffersizemv/4)) [if not already present]
|
実行結果は以下です。
$ ./a.out tol = .1000000000D-11 max_iteration = 10000 Matrix size = 1048576 x 1048576 Check a number of non-zero element idx = 5238785 nz = 5238784 ------------------------------------------------------------- Conjugate gradient without preconditioning ------------------------------------------------------------- iteration= 3531 residual = 9.9760071872183781E-013 CG without preconditioning test is passed Elapased time CG without preconditioning 1.489 (sec) error = 4.1855408028368402E-014 x( 1)=0.499998958505E+00 x( 2)=0.697650643317E+00 x( 3)=0.790607780743E+00 x( 4)=0.841500545499E+00 x( 5)=0.872868905925E+00 x( 6)=0.893963985576E+00 x( 7)=0.909079245320E+00 x( 8)=0.920430160460E+00 x( 9)=0.929263761574E+00 x( 10)=0.936332649288E+00 x(1048566)=0.114542005659E-04 x(1048567)=0.104132673657E-04 x(1048568)=0.937223195617E-05 x(1048569)=0.833110455416E-05 x(1048570)=0.728989537764E-05 x(1048571)=0.624861464650E-05 x(1048572)=0.520727258128E-05 x(1048573)=0.416587940269E-05 x(1048574)=0.312444533254E-05 x(1048575)=0.208298059361E-05 x(1048576)=0.104149540857E-05 |
1048576連立の一次方程式が 3531回の反復で解けており、残差が10^-12以下となっています。
流体シミュレーションへの適用
ここでcuSPARSEを利用して実装した共役勾配法(CG)を流体シミュレーション(CFD)に適用して性能を評価してみました。
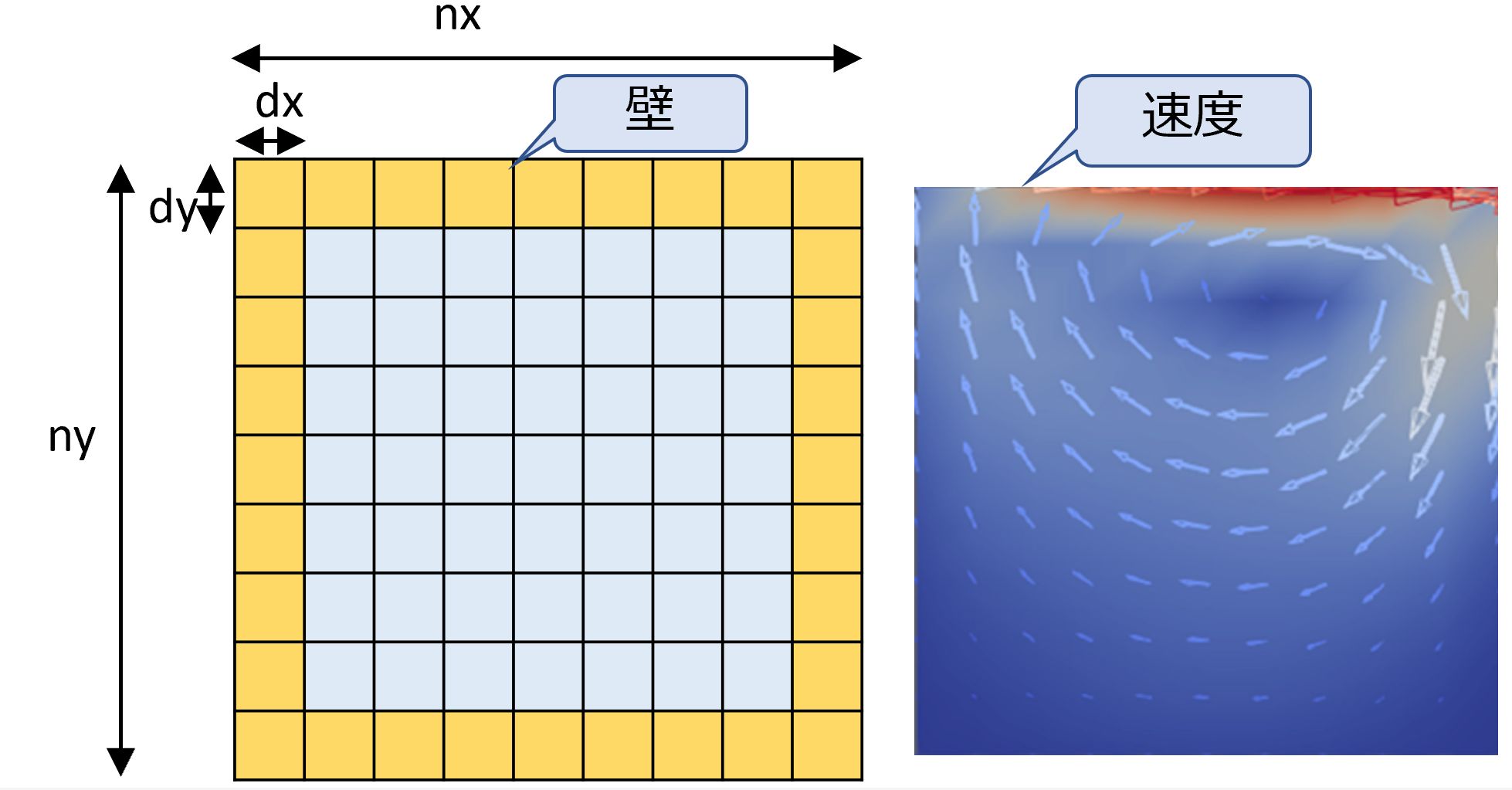
CFDで良く例示される 2次元のCavityモデルにおいて、格子数(nx x ny)を11×11, 101×101, 201×201, 401×401, 801×801と順次拡大して100ステップのシミュレーション時間をGV100 GPUで測定しました。比較対象として、おなじCG処理をBLASおよびIntel MKL(Math Kernel Library)で実装しました。
下記グラフの横軸が格子サイズ、縦軸が実行時間です(実行時間が短いほうが高速)。
青線がCPUでの実行結果、オレンジの線がGPUライブラリを利用した結果です。
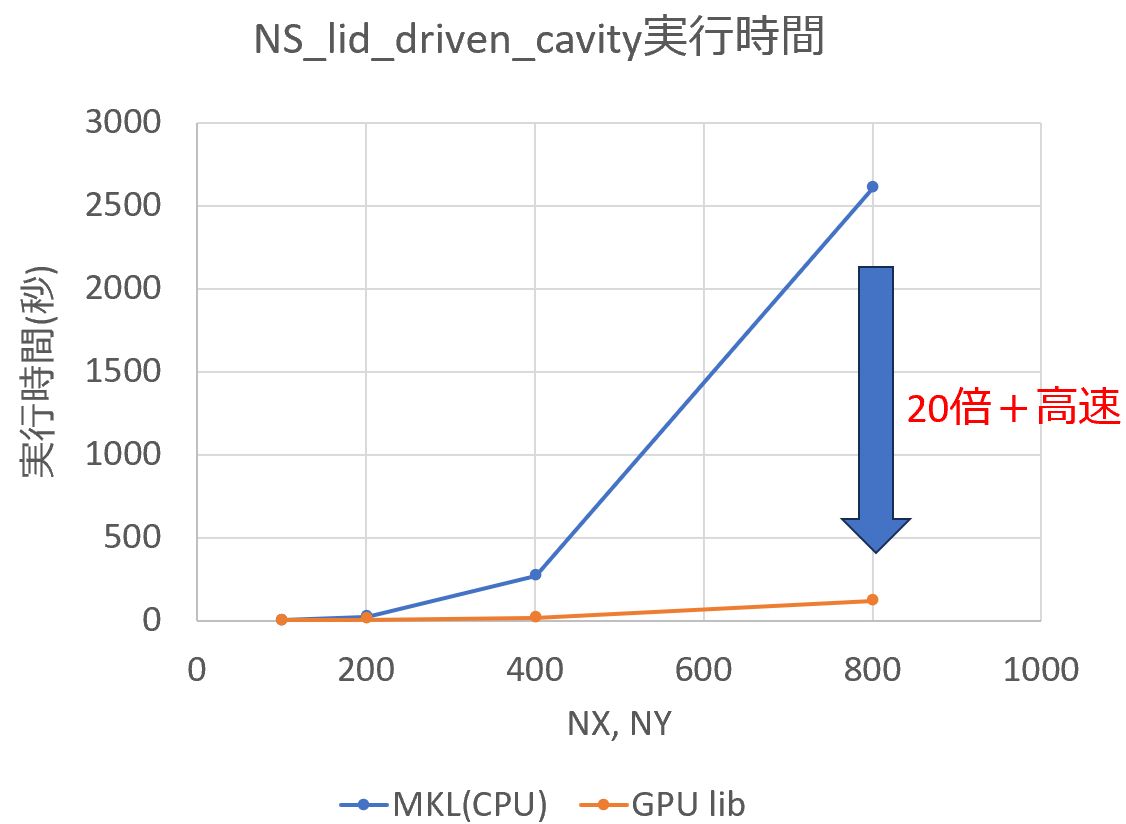
CPU(1コア)実行と比較して、cuBLAS/cuSPARSEでGPUで実行することにより格子サイズ800×800では20倍以上 高速に実行できました。
(グラフからわかるように格子サイズが大きいほどGPUの効果が高いことがわかります)
同じプログラムをA100で実行してみた結果が以下です(緑の線がA100)。
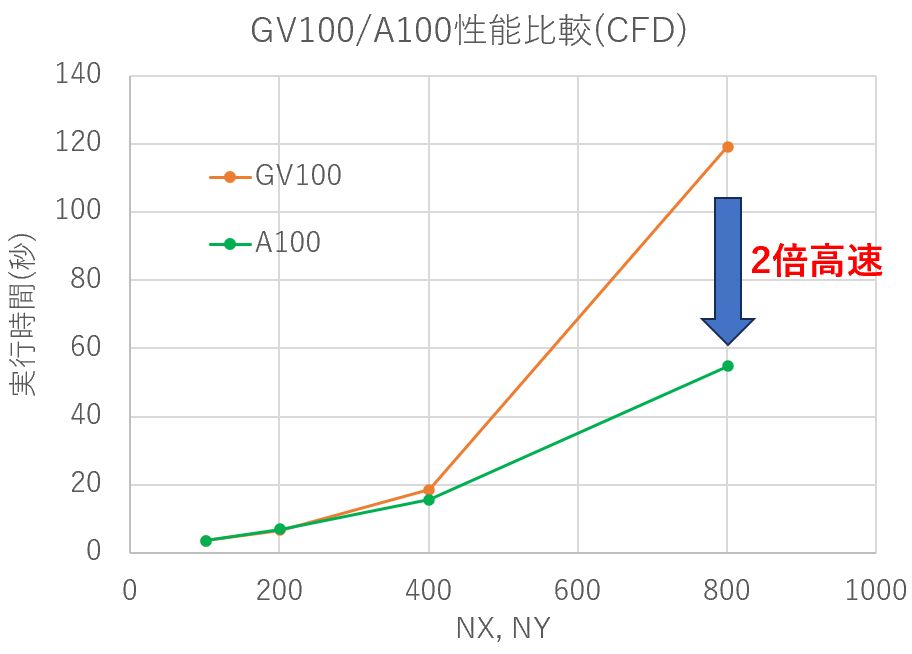
格子サイズ801×801ではA100の性能がGV100に比べて2倍以上高速でした。
(格子サイズが小さい場合はA100とGV100の性能差は小さくなっています)
上記は以下の環境で測定しています(GPUはGV100での性能)
| 製品名 | 理論演算性能 (倍精度浮動小数点演算) |
Clock rate [GHz] |
Memory [GiB] |
core | CUDA version | |
| CPU | Intel(R) Xeon(R) W-2123 CPU | 460.8 GFLOPS | 3.60 | 64 | 4 | |
| GPU | NVIDIA Quadro GV100 (Volta) | 7.4 TFLOPS | 1.627 | 32 | CUDA Cores: 5,120 Tensor Cores: 640 |
11.7 |
| GPU | NVIDIA A100 80GB PCIe(Ampere) | 9.7 TFLOPS | 1.410 | 80 | CUDA Cores: 6,912 Tensor Cores: 432 |
12.2 |
まとめ
GPUライブラリ(cuBLAS, cuSPARSE)を利用して、連立一次方程式の代表的な解法である共役勾配法を実装しました。
cudaは使用せず、GPUへのデータ転送に OpenACC の data clause, host_data clauseのみを使用しました。
BLAS/MKLを利用したCPU 1コア実行とくらべて、GV100で20倍以上高速になりました(格子サイズが大きい場合)。
A100 GPUではGV100の2倍以上の性能が得られる場合もありました。
なお、本内容は GPUプログラミング勉強会 で詳細を紹介させて頂いています(次回9/8金)。
以上

